FAQ

Parsum probes measure the particle size of a single particle, where the statistic chord length acts as a particle attribute. The statistic chord length is obtained by the optical scanning of the projection area of the particle. The particle size is represented by the symbol “x” in accordance with DIN ISO 9276-1. Alternatively, the symbol “d” can also be used.

The displayed quantity measures are the cumulative distribution Q and the density distribution q.

The quantity type is designated with the index “r” in accordance with DIN ISO 9276-1. Since Parsum measuring probes are characterised by a counting-based measurement process, the quantity type is determined by number, with the index r = 0. The length quantity type is indicated by r = 1, the area quantity type by r = 2 and the volume/mass quantity type by r = 3. The measured quantities are the cumulative distribution by number Q0 and the density distribution by number q0.

Measured distributions can be converted to a different quantity type using moments in accordance with DIN ISO 9276-2. The Parsum software calculates the cumulative distribution by volume Q3 and the density distribution by volume q3 from the measured number distributions Q0 and q0.

Since the optical scanning of the projection area of a spherical particle is performed statistically with Parsum probes, the measurement of a sphere with diameter xk gives a frequency distribution of the associated chord lengths in the range of 0 up to xk, with xk being the maximum value.

If the starting distribution is a monodisperse spherical distribution with a sphere diameter of 100 µm, then the diagram will show the density distribution by volume q3 calculated from the measurement of the chord lengths.

The graphical representation used in the Parsum software complies with the specifications of DIN ISO 9276-1. The normalised cumulative distributions by number Q0(x) and by volume Q3(x) range between 0 and 100 %. According to DIN ISO 9276-1, the range 0 to 1 is also possible. If a logarithmic abscissa is used, the values for the relative quantity will remain constant below a certain particle size. The following equation applies: Qr(x) = Qr(ln x). In contrast, the graphical representation of the cumulative distribution does change.

The density distributions q0(x) and q3(x) specified by the Parsum software are determined by correlating the quantity share that falls into a particular particle size interval against the interval width. The quantity share corresponds to the difference between the values of the cumulative distribution at the limits of the interval. For density distributions, the measurement unit [1/µm] applies in the Parsum software. If a logarithmic abscissa is used to display values, the following transformation is performed for the density distribution:

The conversion also applies to the base-10 logarithm. With a logarithmic abscissa, the dimensionless representation of the density distribution is taken from the specified equation.

The starting point here is the conversion of the density distribution q0 to q3. The moments defined in DIN ISO 9276-2 are used for the conversion. The conversion of q0 is performed in particle size intervals by multiplying by the “particle volume” for the relevant particle size interval, expressed by the cube of the number distribution intervals with subsequent normalisation. With the Parsum probe, a number distribution with a resolution of 1 µm is measured “in the original” based on the measurement principle, meaning that each density interval has a unique interval volume that can be used for multiplication. Representation in wider intervals, which can be adjusted for linear representation or in logarithmically distributed interval widths, only occurs as part of the second step when displaying the measurement results. The cumulative distribution Q3 is then calculated by summation of the determined density distribution q3.

If a constant particle density is assumed for sieving, then D(x) = Q3(x) applies to the material that passes through the sieve, and R(x) = 1 – Q3(x) applies to the sieving residue. The sieve intervals are freely adjustable and do not need to comply with a specified sieve series. This ensures that the practical conditions of a wide range of applications can be taken into account. Sieve intervals should be used with which monitoring can be carried out by sieving. This makes the conversion easier.

A width of the particle size interval of 1 µm is used for the measurement and for internal calculations. The interval widths are freely selectable when it comes to presentation.

In the Parsum software, multiple parameters from the cumulative distribution by volume Q3 are presented to indicate the PSD. In accordance with DIN ISO 9276-2, the mean value x50.3 of a cumulative distribution Q3 is defined as follows: Q3(x50.3) = 0.5 (or = 50 %). In analogue mode, additional parameters x1.3, x10.3,…x99.3 are derived. The parameters x10.3, x50.3 and x90.3 are the preferred parameters for presentation.
The user can derive additional parameters from the measurement results themselves, such as the arithmetic mean of the volume diameter:

The user also has the option of checking for use of an approximation function for the measured PSD. By way of example, the parameters n and x‘ for the RRSB distribution can be determined as follows:

The fibre-optic spatial filtering method is a specific version of a spatial frequency filter in the form of a probe. It consists of a lattice arrangement of optical fibres on one side of the measuring volume, and a light source on the other side.

This determines the spatial frequency of single moving particles during the measuring operation. This is performed by projecting the particle movement onto the optical array, with a subsequent frequency analysis of the resulting signal. The velocity of a single particle is calculated from the measured frequency and the known lattice constant of the array.

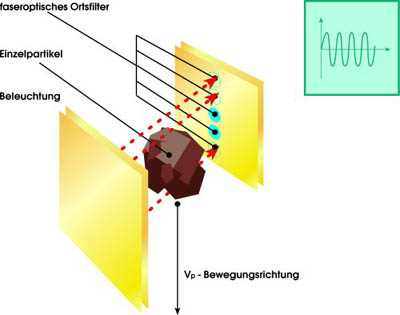
Determination of the particle velocity

Determination of the time of flight

Adding an optical pulse channel to the spatial filter makes it possible to determine the time of flight of a single particle. The particle size in the direction of movement is obtained directly from the time of flight and the velocity.

Online: Continuous measurement in real time. The particles are measured at the same time that they are present within the process. These systems include measuring systems that use a bypass or other extraction systems with or without a return feed.

Inline: The continuous measurement is performed directly within the process. The particles are measured at the same time and at the same location in which they are present within the process.

At-line: The measurement of a sample taken from the process, in the direct vicinity of the process. Taking the samples can be manual or automatic.

Offline: All traditional laboratory analysis methods. A sample is measured at a different time and location from the process.

Our probes are used for inline measurements, i.e., directly within the process, without any sampling or laboratory analysis. The measurement system simultaneously measures the sizes and velocities of particles that pass through the measuring volume of the probe. This method is based on a modified fibre-optic spatial frequency filtering method for measuring particle time of flight and particle velocity.

Single particles are recorded at a high measurement rate that permits a real-time statistical evaluation of particles that are flowing past. The chord lengths are allocated to particle size intervals during data collection. The total number of classified particles is kept constant so that there is a sliding distribution with constantly updated data in real time.

The measured particle numbers in each particle size interval is used as the basis for calculating the density distribution by number q0(x) and the cumulative distribution by number Q0(x) over the chord length x. The software can be used to calculate characteristic particle attributes, such as the median values for particle size x50 and particle speed v50. These values are available for further processing, right through to automated process control via interfaces.

Yes. All methods determine particle size information, so basic comparisons are feasible. However, some special features need to be taken into account to achieve a good approximation of inline and offline PSDs.

1. Avoid errors during sampling: it must be ensured that sampling and the inline measurement are carried out at the same time and location. Depending on the process, a few centimetres of distance between the sampling position and the installation position for inline measurement can lead to significant deviations (such as with sifting effects in pneumatic feed lines, with free-falling bulk goods on ballistic curves).
2. Take into account the special features of continuous measurement. Is the process in a steady state (static) condition? Is the particle size currently increasing/decreasing? Is there a lot of noise in the continuous measurement? (Averaging is required in this case, adaptation of settings, see information on the selection of correct buffer size.)
3. Different measurement methods determine the particle size differently depending on the particle attributes (see next question).

The value referred to as “particle size” by different measurement methods relates to the particle attributes used. These include geometric particle attributes (length, area, volume), the particle mass, the settling speeds of particles and optical particle attributes. In most cases, equivalent diameters are specified, which relate to spheres with the same properties as the particles. For some particle attributes, the deviations are low if the particles are spherical in shape. Parsum probes determine a length attribute using the statistic chord length.

Spatial filter anemometry is a contactless method for measuring the velocity of an object. An image of the moving object is projected onto a photodetector with a spatial filter in front of it. A spatial filter is a gridlike structure mechanically designed as a slit grating, for example. With a fibre-optic spatial filter, the spatial filter consists of a grid-like arrangement of single optical fibres. The output signal of the spatial filter can be described as a superposition of the moving image with a grid function. The photodetector generates a voltage signal with a characteristic frequency, f0, which is proportional to the object velocity, v. The proportional factor is the spatial filter constant, s, which represents the interval between adjacent grid elements. The following applies: v = s•f0 for a magnification of 1. Parsum probes use fibre-optic spatial filter anemometry to measure particle velocities, in order to ultimately determine the statistic chord length in combination with fibre-optic spot scanning of the particle projection area. An introduction to the measuring principle and applications of the spatial filter technique can be found in Y. Aizu and T. Asakura: Spatial Filtering Velocimetry, Fundamentals and Applications p5. 1. edition, Springer-Verlag, Berlin Heidelberg 2006.

Determination of the particle velocity

Determination of the time of flight

Adding an optical pulse channel to the spatial filter makes it possible to determine the time of flight of a particle. The particle size in the direction of movement is obtained directly from the time of flight and the velocity.

SFT: Spatial Filtering Technique

SFV: Spatial Filtering Velocimetry

FSS: Fibre-optic Spot Scanning

With fibre-optic spatial filter anemometry, a collimated beam of light illuminates a moving particle. The shadow of the particle falls onto a spatial filter (grid) made of optical fibres, with the spatial filter constant, s. The optical fibres are connected to a photodetector. The particle velocity, v = f0•s, is derived from the characteristic frequency, f0, of the particle signal.

Fibre-optic spot scanning is the second measurement method used in Parsum probes in addition to fibre-optic spatial filter anemometry. This method involves an impulse being generated at a single optical fibre connected to a photodetector when the shadow projection area of a particle passes by. If the particle velocity is known, then the impulse width can be used to determine the statistic chord length as a measure of particle size.

Parsum probes take consecutive measurements for each single particle within the measuring volume, whereas the laser diffraction method involves recording all of the particles in the measuring volume at the same time. Parsum probes primarily use the number quantity type (r = 0) whereas the laser diffraction method primarily uses the volume quantity type (r = 3).

Particle rates of up to 20,000 particles per second can be recorded. The actual number of particles measured depends on the conditions at the measuring point. A lower data rate is achieved with large, slow-moving particles than with small, fast-moving particles.

The chord length of a single particle is measured with an accuracy of approximately 1 %. The reproducibility of an actual measurement under constant conditions is approximately 1–3 %. The resolution for the particle size distribution parameters is 1 µm.